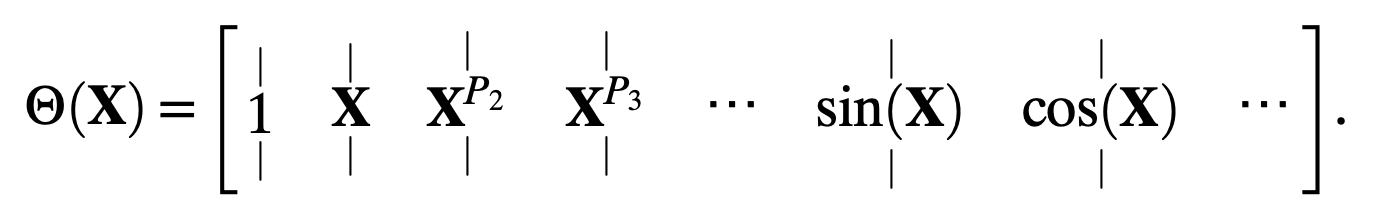Paper summary: Discovering governing equations from data by sparse identification of nonlinear dynamical systems, PNAS, 2016

In short

The SINDy [1] (Sparse Identification of Nonlinear Dynamics) method aims to discover the governing systems of equations of a dynamical system, given noisy measurement data. It is assumed that there are only a few terms in the equations. Therefore, the method leverages group LASSO in order to select a handful of terms out of a large space of candidate functions.

Method

A dynamical system is defined as a system of Ordinary Differential Equations (ODE)

\[\frac{d}{dt}\mathbf{x}_i(t) = \mathbf{f}_i(\mathbf{x}(t)),\]

where $\mathbf{x}(t) \in \mathcal{R}^n$ denotes the state of a system at time $t$, and $\mathbf{f}_i$ represents the governing equation of interest. The goal is to discover $\mathbf{f}$ from the measurements of the state of the system. The data samples at times $t_1, t_2, …, t_m$ are arranged into two matrices:

Then the authors construct the matrix $\mathbf{\Theta}(\mathbf{X})$ which is the evaluation of a large number of non-linear candidate functions on $\mathbf{X}$. For example, $\mathbf{\Theta}(\mathbf{X})$ may include polynomial and trigonometric terms:

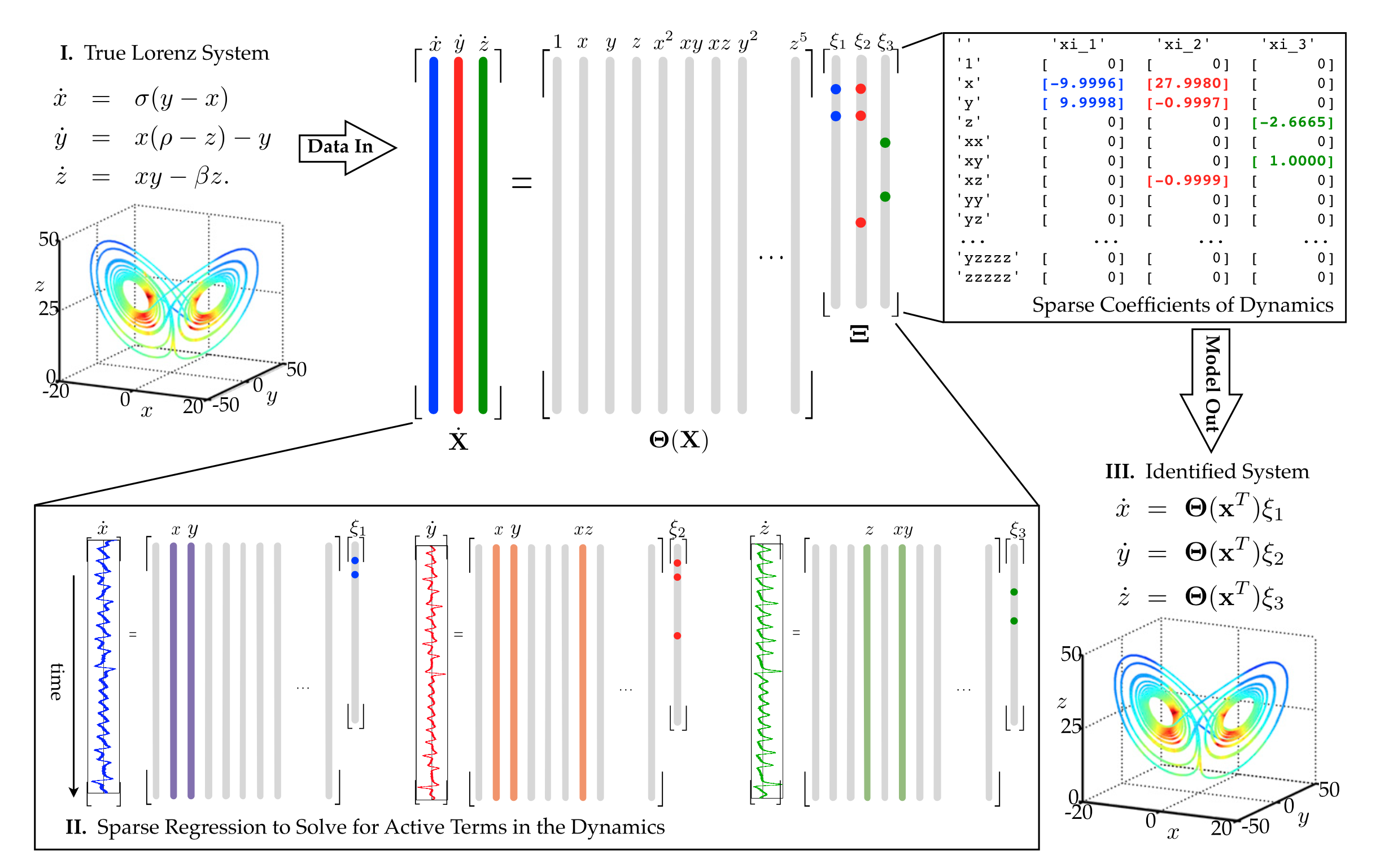
The matrix of derivatives can be measured or approximated numerically. The authors use the total variation regularization method [2] to approximate the derivatives. The matrix of derivatives is linked to the library matrix via the sparse vectors of coefficients $\mathbf{\Xi} = [\mathbf{\xi}_1 \mathbf{\xi}_2 … \mathbf{\xi}_n]$ with

\[\mathbf{\dot{X}} = \mathbf{\Theta}(\mathbf{X})\mathbf{\Xi}.\]

Each column $\mathbf{\xi}_k$ of $\mathbf{\Xi}$ is a sparse vector of coefficients that determines which terms from the library matrix appears in the equation $\dot{x}_k = \mathbf{f}_k(\mathbf{x})$. The following image illustrates the method:

The next step is to infer the matrix of coefficients. Each column $\mathbf{\xi}_k$ requires its own optimization. The authors use LASSO [3] with sequential thresholding to infer $\mathbf{\Xi}$.

References

[1]: Brunton, Steven L., Joshua L. Proctor, and J. Nathan Kutz. “Discovering governing equations from data by sparse identification of nonlinear dynamical systems.” Proceedings of the national academy of sciences 113.15 (2016): 3932-3937.

[2]: Rudin, Leonid I., Stanley Osher, and Emad Fatemi. “Nonlinear total variation based noise removal algorithms.” Physica D: nonlinear phenomena 60.1-4 (1992): 259-268.

[3]: Tibshirani, Robert. “Regression shrinkage and selection via the lasso.” Journal of the Royal Statistical Society Series B: Statistical Methodology 58.1 (1996): 267-288.